# 剑指offer36: 二叉搜索树与双向链表
# 标签:树、链表、搜索树、中序遍历
输入一棵二叉搜索树,将该二叉搜索树转换成一个排序的循环双向链表。要求不能创建任何新的节点,只能调整树中节点指针的指向。
我们希望将这个二叉搜索树转化为双向循环链表。链表中的每个节点都有一个前驱和后继指针。对于双向循环链表,第一个节点的前驱是最后一个节点,最后一个节点的后继是第一个节点。
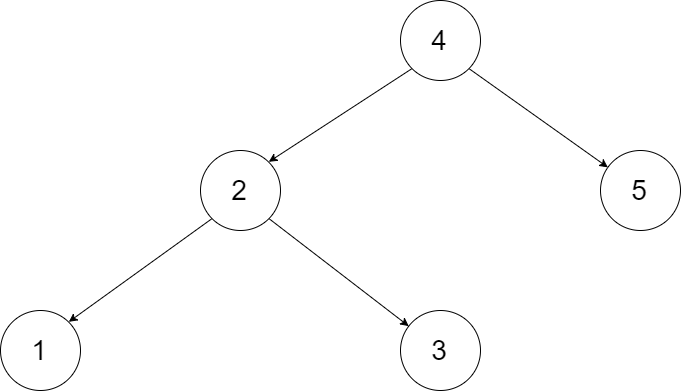
下图展示了上面的二叉搜索树转化成的链表。“head” 表示指向链表中有最小元素的节点。
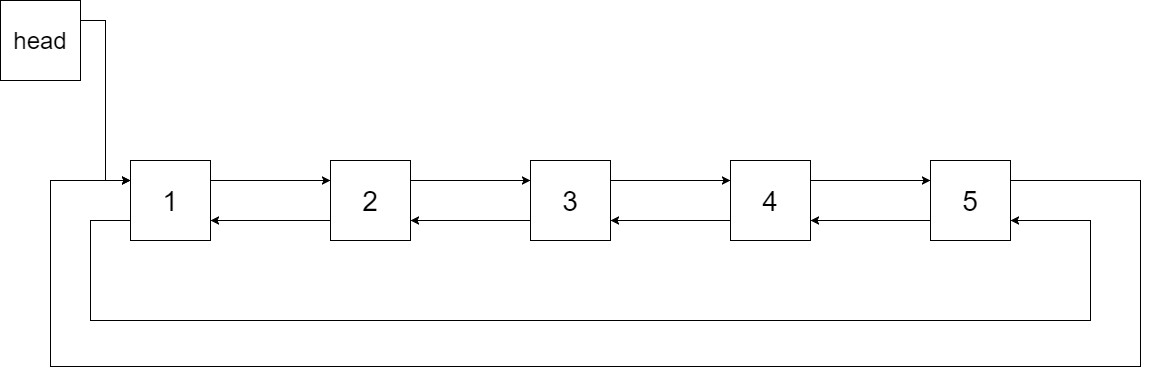
特别地,我们希望可以就地完成转换操作。当转化完成以后,树中节点的左指针需要指向前驱,树中节点的右指针需要指向后继。还需要返回链表中的第一个节点的指针。
# 题解:
我们先来说明一个性质:二叉搜索树的中序遍历为 递增序列。
将二叉搜索树转换成一个排序的循环双向链表,其中包含三个步骤:
- 1 排序链表:节点应该从小到大排序,因此应该使用 中序遍历 从小到大 访问树节点。
- 2 双向链表:在构建相邻节点的引用关系时,设置前驱节点pre和当前节点cur,不仅应该构建
pre.right = cur,还应该构建cur.left = pre - 3 循环链表:设置链表的头节点 head 和尾结点 tail 则应该构建
head.left = tail和tail.right = head
中序遍历对二叉树做 左、根、右的遍历,递归实现如下:
var dfs(node) {
if (node === null) {
return
}
dfs(node.left)
console.log(node.val)
dfs(node.right)
}
1
2
3
4
5
6
7
8
2
3
4
5
6
7
8
对树结构使用递归的方式遍历已经是常规操作。
根据以上的分析,考虑使用中序遍历访问树的各个节点 cur,并且在访问每个节点的时候构建cur和前驱节点pre的引用,中序遍历完成之后,最后构建头结点和尾结点的引用指向即可。
dfs(cur):递归法中序遍历;
- 终止条件: 当节点 cur 为空,代表越过叶子结点,直接返回;
- 递归左子树,即
dfs(cur.left); - 构建链表:
- 当pre为空的时候,代表正在访问链表头节点, 记做head
- 当pre不为空的时候,修改双向节点引用,即 pre.right = cur, cur.left = pre
- 保存 cur: 更新 pre = cur 即节点的cur是后继节点的pre
- 递归右子树,即 dfs(cur.right)
treeToDoublyList(root):
- 特殊处理:如果节点 root 为空,则直接返回
- 初始化 空节点 pre
- 转化为双向链表 调用 dfs(root)
- 构建循环链表
var treeToDoublyList = function(root) {
if (!root) {
return
}
// 头节点
let head = null
// 上一个节点
let preNode = head
// 递归函数
const inOrder = (node) => {
if (!node) {
return
}
// 遍历左子树
inOrder(node.left)
// 处理当前节点
if (!preNode) {
// 遍历到最左边的节点 此时节点就是双向链表的head
head = node
} else {
// 上一个节点的右指针指向当前节点
preNode.right = node
}
// 当前节点的左指针指向上一个节点
node.left = preNode
// 进入下一轮循环之前把上一个节点的指针指向当节点
preNode = node
// 遍历右子树
inOrder(node.right)
}
inOrder(root)
// 完成中序遍历之后,pre指向了最后一个节点,head指向头节点,
// 因为是循环链表,所以头节点的左指针指向最后一个节点,最后一个节点的右指针指向头节点
head.left = preNode;
preNode.right = head;
return head;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
这道题目牛客上也有类似的题目,但是问法不一样,牛客上的题目,最终并不要求头节点和尾结点相连,仅仅是中间的部分转化为双向链表。